Widerstände kombinieren
Mehrere Widerstände lassen sich zu neuen Werten kombinieren. So kann man Widerstände zusammensetzen,
die es in den Normreihen nicht gibt. Nützlich ist das auch, wenn der Kollege wieder mal den letzten
Widerstand aus der Schublade genommen hat, ohne neue zu bestellen.
Durch geschicktes kombinieren von nur drei Widerständen lässt sich jeder gewünschte Wert ziemlich genau erreichen. Man muss dazu nur ein paar wenige Grundschaltungen kennen und sie berechnen können.
Durch geschicktes kombinieren von nur drei Widerständen lässt sich jeder gewünschte Wert ziemlich genau erreichen. Man muss dazu nur ein paar wenige Grundschaltungen kennen und sie berechnen können.
Zwei Widerstände kombinieren
Die einfachste Art, Widerstände zu kombinieren, ist eine Reihen- oder Parallelschaltung aus zwei Widerständen.
Bei der Reihenschaltung ist die Berechnung am einfachsten: Der Gesamtwiderstand besteht aus der
Addition der Einzelwiderstände. In der Reihenschaltung ist der Gesamtwiderstand deshalb immer grösser
als der grösste der einzelnen Widerstände.
Beim Kombinieren von zwei Widerständen zu einer Parallelschaltung ist die Berechnung etwas komplizierter. Der Gesamtwiderstand ist der Kehrwert aus der Addition der Kehrwerte der Einzelwiderstände. In der Parallelschaltung ist der Gesamtwiderstand immer kleiner als der kleinste Einzelwiderstand.
Für die Berechnung findest du auch hilfreiche Tools auf den Rechnerseiten: Für die Serieschaltung und für die Parallelschaltung.
Beim Kombinieren von zwei Widerständen zu einer Parallelschaltung ist die Berechnung etwas komplizierter. Der Gesamtwiderstand ist der Kehrwert aus der Addition der Kehrwerte der Einzelwiderstände. In der Parallelschaltung ist der Gesamtwiderstand immer kleiner als der kleinste Einzelwiderstand.
Für die Berechnung findest du auch hilfreiche Tools auf den Rechnerseiten: Für die Serieschaltung und für die Parallelschaltung.
Bild 1: Zwei Widerstände kombinieren mit Serie- und Parallelschaltung
Drei Widerstände kombinieren
Ist der gewünschte Widerstand mit dem Kombinieren von zwei Widerständen nicht erreichbar, bringt es
einem meistens zum Ziel, drei Widerstände zu kombinieren. Die Formeln der Serie- und der Reihenschaltung
können einfach um einen Widerstand erweitert werden.
Der Autor empfiehlt übrigens beim Kombinieren von Widerständen, die Parallelschaltung zu verwenden. Sie ist zwar etwas schwieriger zu berechnen, aber schlussendlich ist sie übersichtlicher, weil sie keine neuen Spannungsknoten bieten. Die parallel kombinierten Widerstände sind einfach besser als zusammengehörend zu erkennen.
Der Autor empfiehlt übrigens beim Kombinieren von Widerständen, die Parallelschaltung zu verwenden. Sie ist zwar etwas schwieriger zu berechnen, aber schlussendlich ist sie übersichtlicher, weil sie keine neuen Spannungsknoten bieten. Die parallel kombinierten Widerstände sind einfach besser als zusammengehörend zu erkennen.
Bild 2: Drei Widerstände kombinieren mit Serie- und Parallelschaltung
Die Serie- und die Parallelschaltung lässt sich beliebig erweitern. Für einen 29 kOhm Widerstand
könnte man zum Beispiel 29 1kOhm Widerstände in Serie schalten. Dies ist aber weder sinnvoll
und praktisch. Besser versucht man es mit einer gemischten Schaltung:
Gemischte Schaltungen mit drei kombinierten Widerständen
Gemischte Schaltungen sind Schaltungen, bei denen Widerstände seriell und parallel kombiniert sind.
Mit drei Widerständen lassen sich die beiden einfachsten gemischten Widerstandsschaltungen kombinieren:
Die eine besteht aus einem Seriewiderstand zu zwei parallelen Widerständen.
Die andere ist ein paralleler Widerstand zu zwei seriell geschalteten Widerständen.
Mit diesen kombinierten Widerständen lassen sich extrem genaue Gesamtwiderstände erreichen, auch wenn die Berechnung etwas umständlich ist.
Die eine besteht aus einem Seriewiderstand zu zwei parallelen Widerständen.
Die andere ist ein paralleler Widerstand zu zwei seriell geschalteten Widerständen.
Mit diesen kombinierten Widerständen lassen sich extrem genaue Gesamtwiderstände erreichen, auch wenn die Berechnung etwas umständlich ist.
Bild 3: Mit gemischen Schaltungen drei Widerstände kombinieren
Um zum vorherigen Beispiel vom gewünschten 29 kΩ Widerstand zurückzukommen:
Wählt man die seriellen R1 = 27kΩ und R2 =2.2kΩ, so hat man 29.2kΩ. Man ist also schon recht nahe dran.
Kombiniert man parallel zu R2 noch einen R3 von 22kΩ, ergibt die Parallelschaltung (R2//R3) einen Wert von genau 2kΩ.
Damit ergibt R1 + (R2//R3) = 27kΩ + 2kΩ = 29kΩ.
Wie man diese Schaltungen dimensionert und die richtigen Widerstandskombinationen findet ist etwas Übungssache. Jeder Elektroniker entwickelt mit der Zeit sein eigenes Vorgehen um gute Kombinationen zu finden.
Wählt man die seriellen R1 = 27kΩ und R2 =2.2kΩ, so hat man 29.2kΩ. Man ist also schon recht nahe dran.
Kombiniert man parallel zu R2 noch einen R3 von 22kΩ, ergibt die Parallelschaltung (R2//R3) einen Wert von genau 2kΩ.
Damit ergibt R1 + (R2//R3) = 27kΩ + 2kΩ = 29kΩ.
Wie man diese Schaltungen dimensionert und die richtigen Widerstandskombinationen findet ist etwas Übungssache. Jeder Elektroniker entwickelt mit der Zeit sein eigenes Vorgehen um gute Kombinationen zu finden.
X
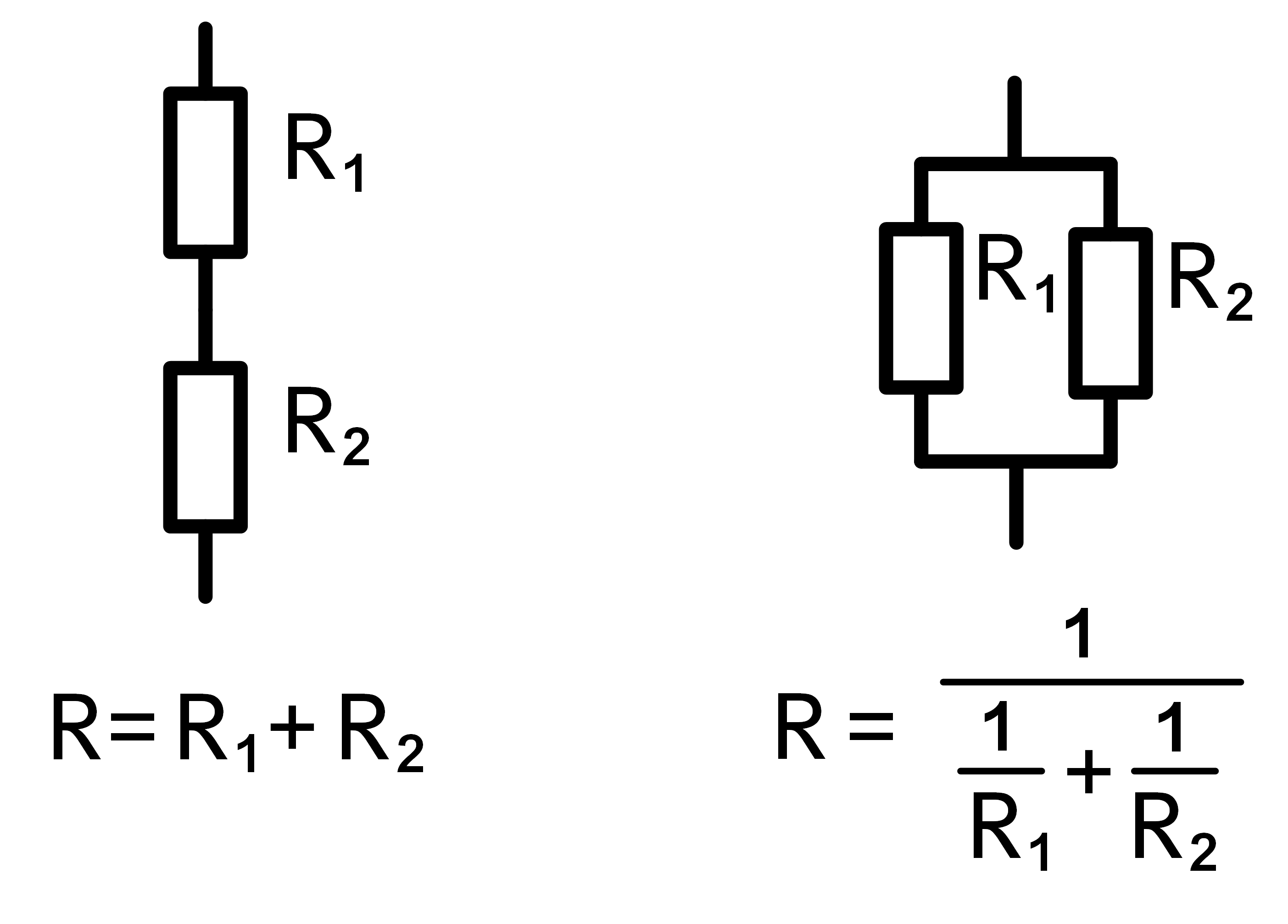
Bild 1: Zwei Widerstände kombinieren mit Serie- und Parallelschaltung
Bild 1: Zwei Widerstände kombinieren mit Serie- und Parallelschaltung
X
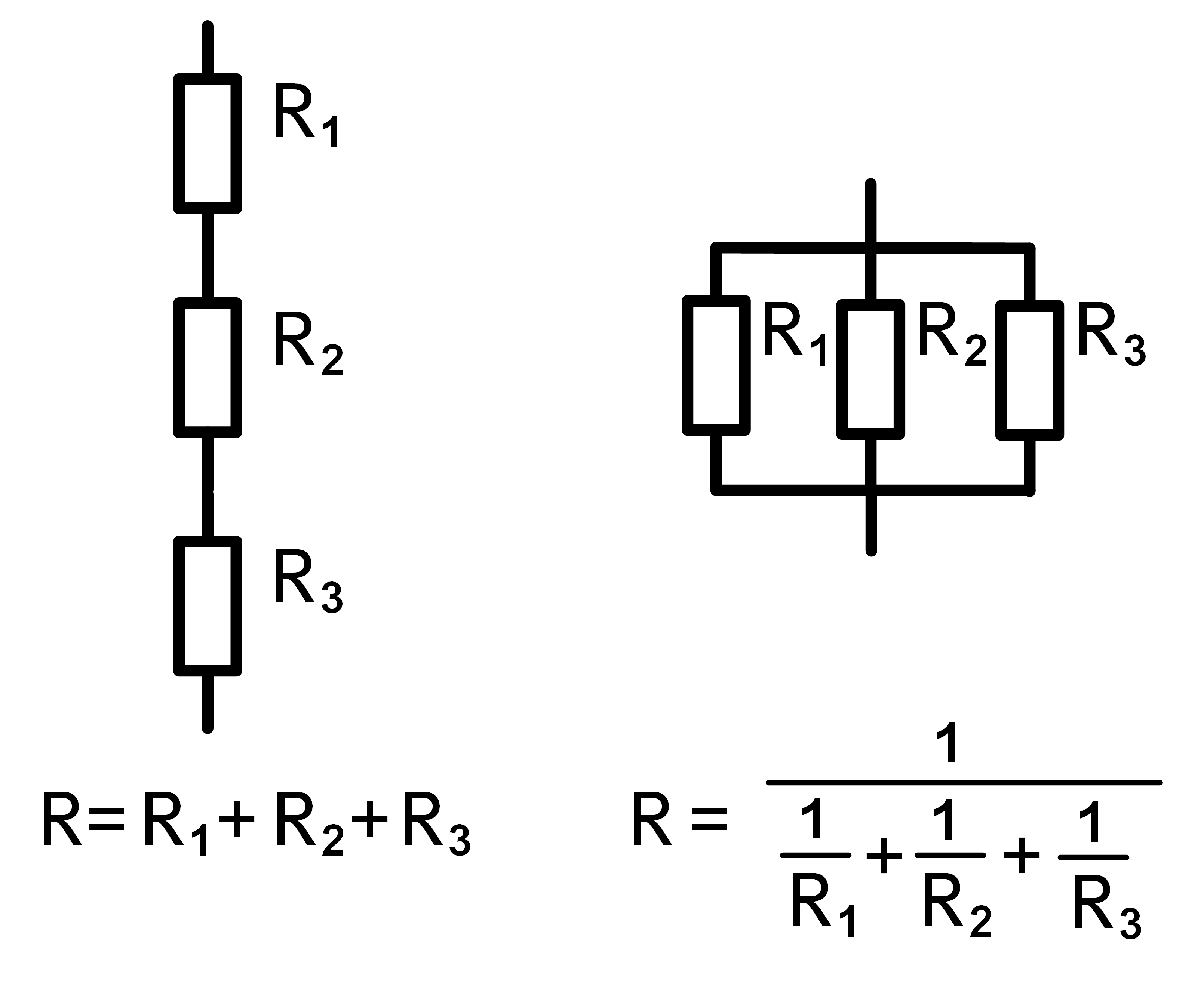
Bild 2: Drei Widerstände kombinieren mit Serie- und Parallelschaltung
Bild 2: Drei Widerstände kombinieren mit Serie- und Parallelschaltung
X
Bild 3: Mit gemischen Schaltungen drei Widerstände kombinieren
Bild 3: Mit gemischen Schaltungen drei Widerstände kombinieren
Das könnte dich auch langweilen:
Nützliche Tools
Elektronik Rechner online
Bauteilkunde
Widerstand Farbcode
Nur für wahre Nerds
Electronicsplanet Roboterprojekte
Tipps für Newbies
Farbcode Leserichtung bestimmen